نظرية {1} :
طول القطعة المستقيمة الواصلة بين رأس القائمة ومنتصف الوتر في المثلث قائم الزاوية يساوي نصف طول الوتر.
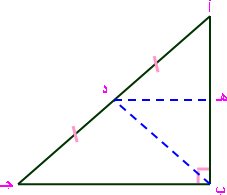
المعطيات: أ ب ﺠ مثلث قائم الزاوية في ب ، النقطة (د) منتصف أ ﺠ ، وصل راس القائمة بالنقطة (د)
أ ﺠ
.
|
 |
المطلوب:
إثبات أن
ب د
=
|
العمل :
أنزل د
ﻫ
عمود على
أ ب .
البرهان :
نبحث في
تشابه المثلثين أ
ﻫ
د ، أ ب
ﺠ
.
(90
ْ
) ،
|
أ ب
ﺠ
=
|
 |
أ
ﻫ
د
=
|
|
أ مشتركة بين المثلثين .
|
|
المثلثان
أ
ﻫ
د ، أ ب ﺠ
متشابهان .
أ ب
.
|
|
ومنه نستنتج أن
أ
ﻫ =
|
|
=
|
 |
أي
أ ﻫ = ﻫ ب
.
والآن نبحث
في تطابق المثلثين أ ﻫ د و ب د ﻫ .
ب
ﻫ
د
= 90 ْ ،
ﻫ
د مشترك .
|
|
أ
ﻫ
د
=
|
|
أ
ﻫ
=
ب
ﻫ
،
|
\
ينطبق المثلثان بضلعين وزاوية محصورة بينهما ،
أ
ﺠ
.
|
|
وينتج أن
أ د = ب د
لكن
أ د
=
|
أ
ﺠ
............ وهو المطلوب .
|
|
أ ي
ب د =
|
|
..................................................................................................................................................................
.......................................................................................................................................................................
نظرية {2}:
طول القطعة المستقيمة الواصلة بين منتصفي ضلعين في مثلث يساوي نصف طول الضلع الثالث.
المعطيات :
أ
ب ﺠ
مثلث : النقطتان د ،
ﻫ
منتصف
أ ب
، أ
ﺠ
على الترتيب .
ب
ﺠ
.
|
 |
المطلوب :
إثبات 1) د ﻫ
|
ب
ﺠ
.
|
|
2)
د ﻫ =
|
البرهان :
في المثلثين أ د
ﻫ
،
أ ب
ﺠ
الزاوية
أ
مشتركة .
، الزاوية أ مشتركة
.
|
|
=
|
 |
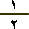أ د
ﻫ
وهما في موضع التناظر .
|
|
أ ب
ﺠ
=
|
|
\
المثلثان متشابهان وينتج من ذلك أن
|
ب
ﺠ
.
|
|
\
د
ﻫ
|
.
|
|
=
|
 |
ومن التشابه أيضاً نستنتج أنّ :
|
| البرهان .............. |
.
.....................................................................................................................................................
........................................................................................................................................................
نظرية {3}:
مربع الوتر = مربع الضلع الأول + مربع الضلع الثاني.
ملاحظة : هذه النظرية مهمة وتفيد في حل الكثير من المسائل في الرياضيات.
 |
| فيثاغورس صاحب النظرية ........................................................................ .............................................................................. نظرية {4}: قطراا متوازي الأضلاع ينصف كل منهماا الآخر. يمكنك اثبات هذه النظرية بمساعدة الشكل التالي،حيث اننا افترضناا الاحداثيات بشكل صحيح وبالتالي بقي أن نجد احداثيات المنتصف لكل قطر بناء على القانون المعروف س1+س2 مقسومة على العدد 2 ، وص1 +ص2 مقسومة على 2 أيضا وسوف تكون نتيجة الحل أن احداثيات منتصف كل قطر منهماا نفس الاحداثيات وبالامكان ان نفترض أن هذه النقطة التي تنصف القطرين مثلا د .  ملاحظة هامة بخصوص احداثيات النقطة ب . انظر الي الشكل التالي ان القاعدتين المشار لهما باللون الازرق بالدوائر متساويتان كما ان وشكل المتوازي ناتج عن الازاحة لذلك فاللاحداثي السيني للنقطة ب كان س1 + س2  | ز |
نظرية {5}:
طول القطعة الواصلة بين منتصفي الضلعين غير المتوازيين في شبه المنحرف ، يساوي نصف مجموع طولي القاعدتين المتوازيتين فيه .
ولمعلوماتك فان من خصائص شبه المنحرف
- يكون فيه ضلعين متقابلي نمتوازيين، والضلعين الآخرين متساويين في الطول.
- يكون طول قطريه متساويين. *تكون زاويتا القاعدتين متطابقتين.
ليست هناك تعليقات:
إرسال تعليق